GitHub Actionsのself-hosted runnersをDockerで作ってみる

こんばんは。
ずっと暑いですね。外に出ると溶けそうになります。

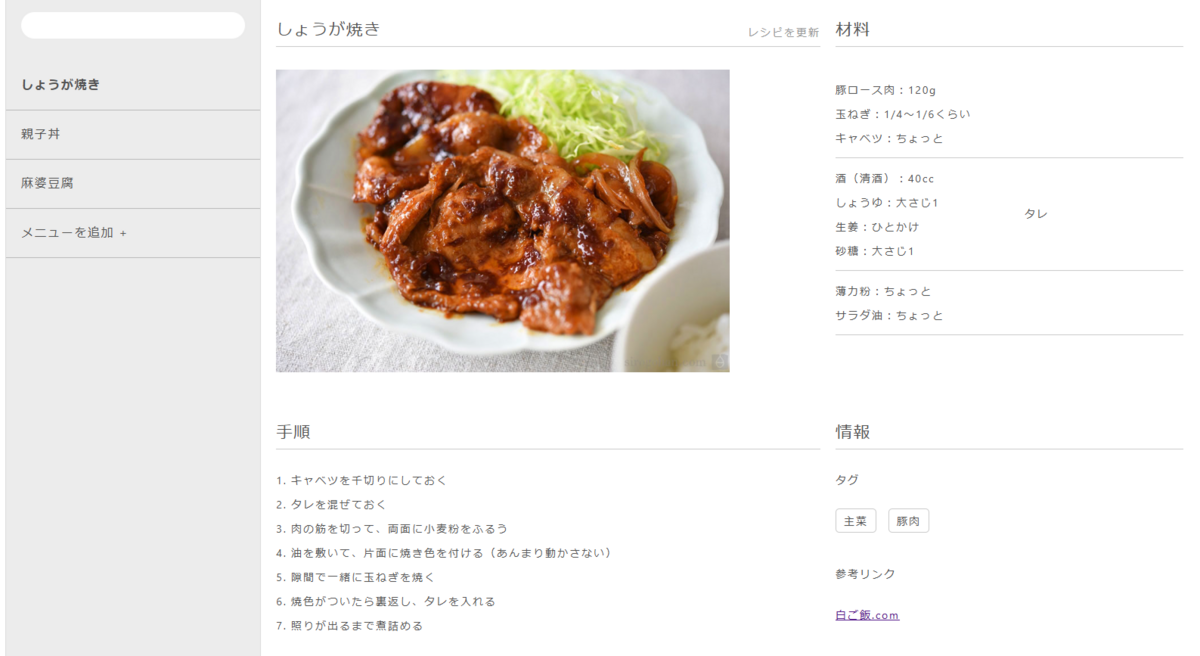
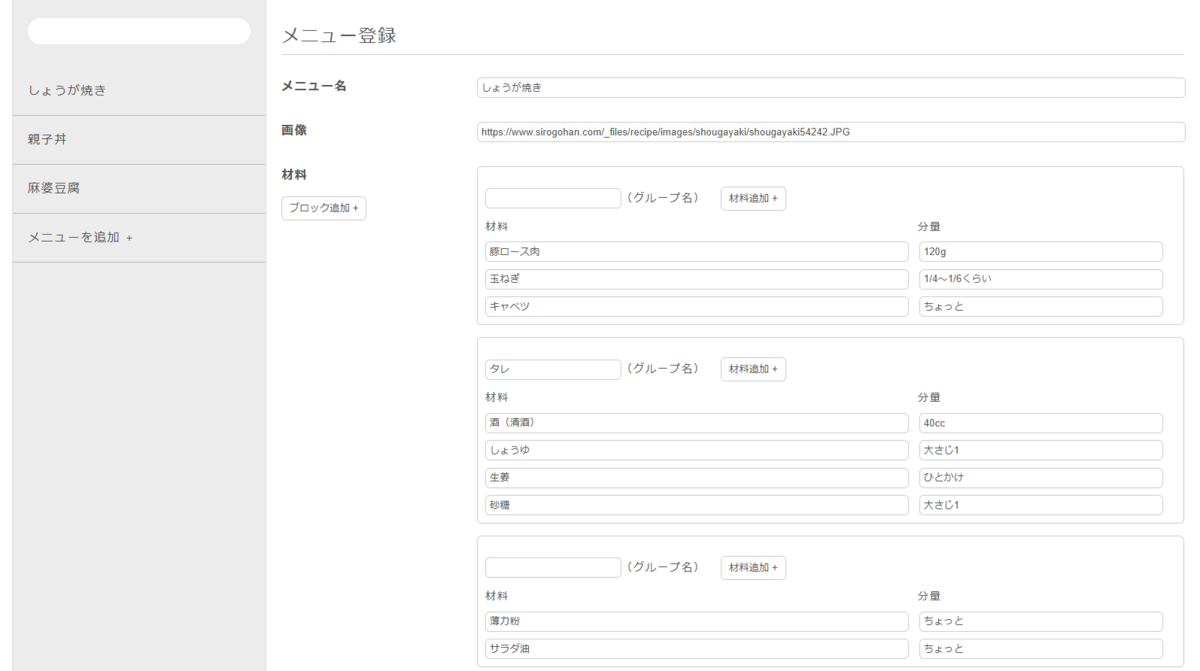
さて、最近はCI/CDといえばGitHub Actionsが結構有力な選択肢ですが、そういえば自分で構築したことがなかったなと思って試してみます。
前半はポチポチ触っていますが、後半に最終的なDockerfileの設定もあるので、場合によっては読み飛ばしてください。

self-hosted runnersってなんぞや

GitHub Actionsではpushやpull requestといったイベントをトリガーに任意のワークフローを実行することができます。
GitHubが用意してくれている環境を「github-hosted runners」、自分で用意する環境を「self-hosted runner」といいます。

github-hosted runnersはAzureの仮想マシンで動いているらしいですね。
パブリックリポジトリなら無制限、プライベートリポジトリだと無料枠があるようです。（Freeだと2000分/月）
GitHub Actions の課金について - GitHub Docs

self-hosted runnerはHTTPSのロングポーリングを使ってランナー側からGitHub側にアクセスしているので、ポート開放やIPアドレスの割当等が不要なあたりがとても便利です。

作るならDockerがいい

というわけで自宅のLinuxサーバにDockerを使ってself-hosted runnerを建ててみます。

手順を確認

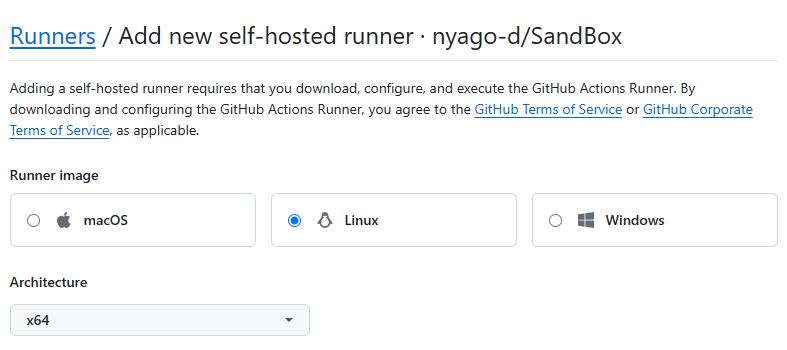
まずは対象としたいリポジトリのSettings>Actions>Runnersから「New self-hosted runner」ボタンを押します。

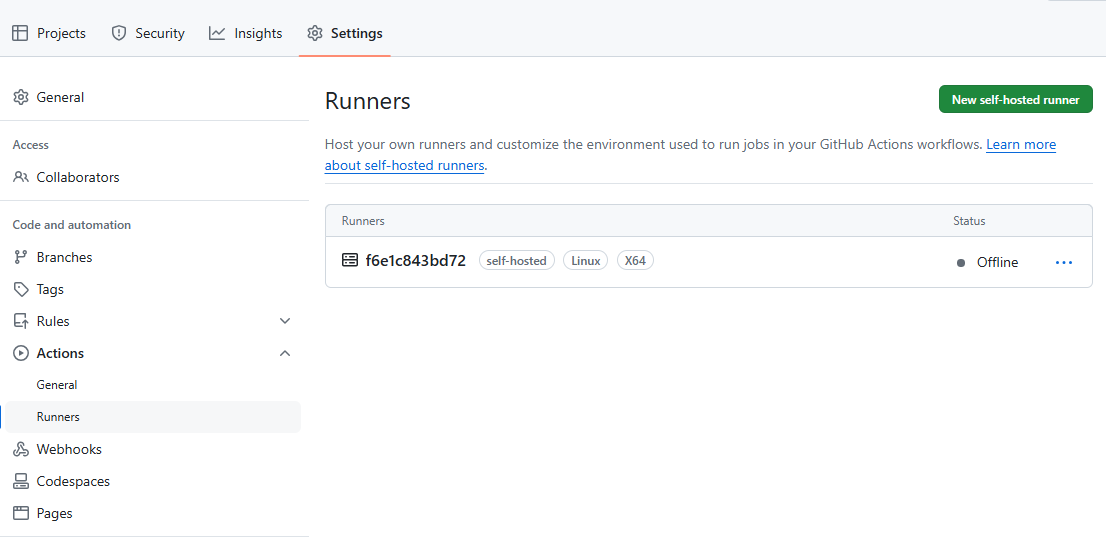
自身の環境を選択します。今回の私の場合はRunner imageがLinuxでArchitectureがx64です。
LinuxでArchitecutureがよくわからない場合は「uname -a」コマンドとかを叩いてみるとよいかと思います。間違えると後で面倒なので先に確認しましょう。（ハマった人）

コンテナの準備

最初からDockerfileを書きたい気持ちもあるのですが、なんだかつまづきそうな気がするのでひとまずプレーンにコンテナを建ててコマンドを叩いていくことにします。

Dockerfile

FROM ubuntu:24.04

docker-compose.yml

version: '3.8'
services:
  self_hosted_runner:
    build: .
    container_name: self_hosted_runner
    tty: true
    stdin_open: true

上記の2ファイルを適当なフォルダに作ったら以下のコマンドを叩いて、コンテナの起動&コンテナの中に入ります。

docker compose up -d
docker exec -it self_hosted_runner /bin/bash

手順に沿って作業

基本的には画面に記載のコマンドのとおり実行していくのですが、なんだかんだあれが足りないとかこれが違うとか言われます。
インストールが必要になるのはsudoとcurlなので、先にapt-getを更新したうえでインストールしておきます。

apt-get update
apt-get install -y sudo curl

次にGitHubのページに従ってダウンロードまで済ませます。ハッシュのチェックはお好みらしいので一旦省略。（インストールするもの増えるので）

mkdir actions-runner && cd actions-runner
curl -o actions-runner-linux-x64-2.317.0.tar.gz -L https://github.com/actions/runner/releases/download/v2.317.0/actions-runner-linux-x64-2.317.0.tar.gz
tar xzf ./actions-runner-linux-x64-2.317.0.tar.gz

あとは設定のシェルを実行すればOKと思いきや、

./config.sh --url https://github.com/{user}/{repository} --token {token}

rootユーザじゃダメだよ的なことを言われます。

Must not run with sudo

仕方がないのでユーザを作ります。このユーザをsudoグループに入れて最初からこのユーザを使うのもありですが、今回はつけないでおきます。

useradd -m runner -s /bin/bash
su runner

で、改めて実行すると

./config.sh --url https://github.com/{user}/{repository} --token {token}

依存関係が不足しているから、インストール用のシェルを叩いてと言われます。
が、何故かこれを実行しても問題が解決しません。（rootで実行とrunnerユーザにsudo権限つけて実行の両方試したけどダメでした…何故…）

Libicu's dependencies is missing for Dotnet Core 6.0
Execute sudo ./bin/installdependencies.sh to install any missing Dotnet Core 6.0 dependencies.

仕方がないので足りないと言われているLibicuを自分でインストールします。

exit   # rootに戻る
apt-get install -y libicu-dev
su runner

今度こそ実行できるようになります。

./config.sh --url https://github.com/{user}/{repository} --token {token}

なんかこんな感じにいろいろなことを聞かれます。（Enterポチポチで良きに計らってくれます）

--------------------------------------------------------------------------------
|        ____ _ _   _   _       _          _        _   _                      |
|       / ___(_) |_| | | |_   _| |__      / \   ___| |_(_) ___  _ __  ___      |
|      | |  _| | __| |_| | | | | '_ \    / _ \ / __| __| |/ _ \| '_ \/ __|     |
|      | |_| | | |_|  _  | |_| | |_) |  / ___ \ (__| |_| | (_) | | | \__ \     |
|       \____|_|\__|_| |_|\__,_|_.__/  /_/   \_\___|\__|_|\___/|_| |_|___/     |
|                                                                              |
|                       Self-hosted runner registration                        |
|                                                                              |
--------------------------------------------------------------------------------

# Authentication


√ Connected to GitHub

# Runner Registration

Enter the name of the runner group to add this runner to: [press Enter for Default]

Enter the name of runner: [press Enter for f6e1c843bd72]

This runner will have the following labels: 'self-hosted', 'Linux', 'X64'
Enter any additional labels (ex. label-1,label-2): [press Enter to skip]

√ Runner successfully added
√ Runner connection is good

# Runner settings

Enter name of work folder: [press Enter for _work]

√ Settings Saved.

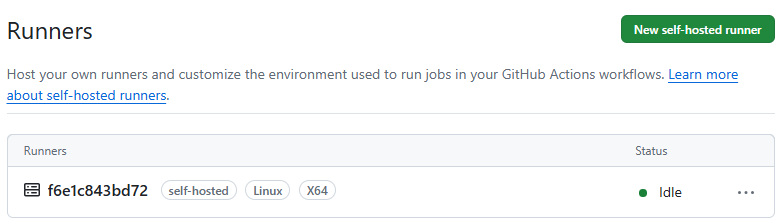
これで設定が完了したので、あとは起動のシェルを叩けば待受状態になります。

./run.sh

√ Connected to GitHub

Runnerが作られて状態がIdleになっています。

Dockerfileにまとめよう

せっかくDockerを使っているのでまとめてみます。
RUNをどこまで繋げるものなのかよくわからない…繋げられる場合は全部繋げてしまっていいのだろうか。

Dockerfile

FROM ubuntu:24.04

RUN apt-get update \
 && apt-get install -y sudo curl libicu-dev

RUN useradd -m runner -s /bin/bash

RUN mkdir actions-runner && cd actions-runner \
 && curl -o actions-runner-linux-x64-2.317.0.tar.gz -L https://github.com/actions/runner/releases/download/v2.317.0/actions-runner-linux-x64-2.317.0.tar.gz \
 && tar xzf ./actions-runner-linux-x64-2.317.0.tar.gz 

USER runner
WORKDIR /actions-runner

RUN ./config.sh \
      --url https://github.com/{user}/{repository} \
      --token {token} \
      --unattended \
      --name sample-runner

CMD ["./run.sh"]

docker-compose.yml

version: '3.8'
services:
  self_hosted_runner:
    build: .
    container_name: self_hosted_runner

これで「docker compose up -d」一発でランナーの立ち上げまでできるようになりました。
中身ほとんどないのでdocker composeじゃなくてもいいかもしれないです。

試しにWorkflowを動かしてみる

とりあえず動作確認がしたいので、すごくシンプルなワークフローを作ります。
今回は「workflow_dispatch」を指定しているので、手動でトリガーする形です。
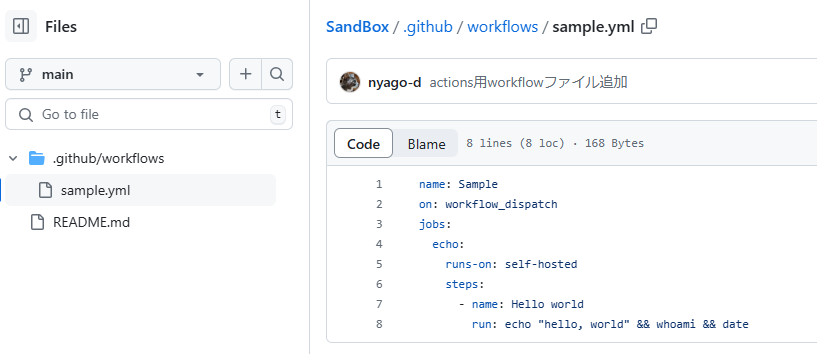
./github/workflows/sample.yml

name: Sample
on: workflow_dispatch
jobs:
  echo:
    runs-on: self-hosted
    steps:
      - name: Hello world
        run: echo "hello, world" && whoami && date

こんな感じ。

Actionsタブにワークフローが表示されるようになります。

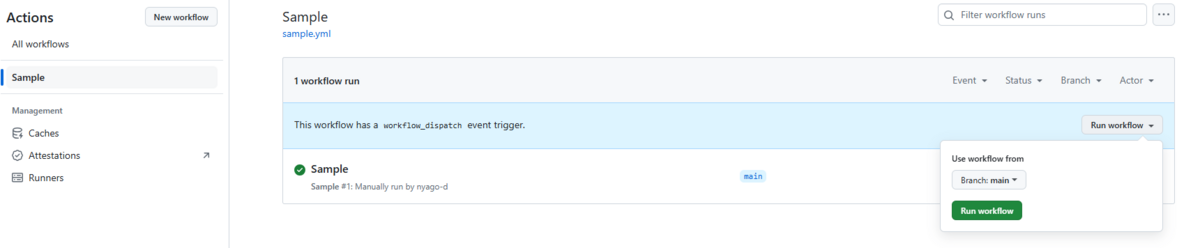
Run workflowで実行すると、無事に実行されたようです。

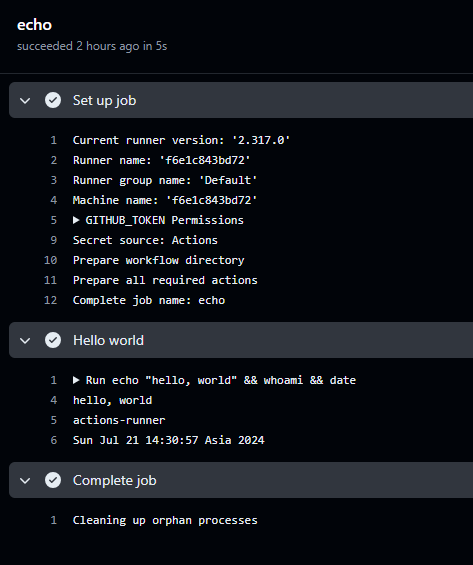
ランナー側にはこんな感じでコンソール出力されていました。

2024-07-21 14:30:52Z: Running job: echo
2024-07-21 14:31:03Z: Job echo completed with result: Succeeded

わりとすんなり感はあったけれど

環境構築はなんだかんだでハマりますね…。
でも、設定のシェルが叩けるようになったあとは「もうつながったの？」という感じのすんなりさでした。

今回はちょっとした処理を試しただけですが、実際に利用するのであればDinDを使ってコンテナを綺麗に保ったり、DooDを使って別のリソースにアクセスしたりみたいな工夫が必要になってきそうですね。
（DooDについては以前の記事があるので良ければ参考に）

正直現状だと家でCI/CDちゃんとしたいような使い方をしていないので何ともですが、外からアクセスできることを生かした面白いことができたりしないもんかなと思っています。
外出先からVPNを有効にするとかできたら便利そうかなくらい…？何かないかな。

それでは。

2024年上半期に読んだ本からおすすめを紹介

こんばんは。
気づけばもう6月も終わり、なんと1年の半分が終わってしまいました。

この半年で読んだ本のうち、良かったものを簡単な感想とともに紹介します。
まとめてじゃなくて読むたびに書いた方がいいんだろうなと思ったり…せめて2か月くらいペースしようかな。

前回のはこちら

shironeko.hateblo.jp

ビジネス・マネジメント

GitLabに学ぶ 世界最先端のリモート組織のつくりかた

GitLabに学ぶ 世界最先端のリモート組織のつくりかた ドキュメントの活用でオフィスなしでも最大の成果を出すグローバル企業のしくみ

リモートでもパフォーマンスが出るというメンバーと、やっぱり出社とのパフォーマンスの乖離を感じる管理職みたいな対立はよくあると思います。
もちろんリモートに働く上での様々なメリットがあるというのは理解した上で、だからといって根拠のないリモートで大丈夫というのではなく、リモートでちゃんと成果が出る仕組みをつくっていく形にしていく必要があるなと考えさせられました。

だから僕たちは、組織を変えていける

だから僕たちは、組織を変えていける ――やる気に満ちた「やさしいチーム」のつくりかた【ビジネス書グランプリ2023「マネジメント部門賞」受賞！】

組織がただの人の集まりでないことはわかっていても、その組織を良い組織にしていくことは簡単なことではないです。
「ミッション・ビジョン・バリュー」「心理的安全性」「メンタルモデル」といったよく耳にするワードを交えながらも、組織を形作る様々な視点に触れていてとても学びがありました。
「学習する組織」「共感する組織」「自走する組織」といった組織の特徴の対比についてもなかなか面白いです。

戦略の要諦

戦略の要諦 (日本経済新聞出版)

「良い戦略、悪い戦略」のリチャード・Ｐ・ルメルト氏の新しい本です。引き続き選択と集中による戦略の大切さを語る内容ではありますが、またちょっと違ったベクトルから戦略を語っています。
前作が戦略を伴わない目標には意味がないという構造についての話だとするならば、今作は観測から現実性を持って建てた戦略が目標につながるという時系列の流れが意識されているように個人的には感じました。
もちろん組織という目線で見たときに目標は下位の組織に具体化しながら派生してく必要はあるのですが、その上位の目標を形作るためのボトムアップの観測は確かに重要だなと最近ちょっと意識しています。

Data is BOSS

DATA is BOSS 収益が上がり続けるデータドリブン経営入門

データドリブンとはどういうことなのかということがわかりやすく語られています。
データを活用しようというのはいまどきどこの会社でも言っているようなことではありますが、YoYを見て100%に届きませんでしたもっと頑張ろうとか、競合に負けているからとにかく真似をしようとか、意味のあるデータ分析ができていることはとても稀なように思えます。

本書でのデータドリブンとは、顧客ドリブンとほぼ同じ意味です。本書内の「データ」という言葉を「顧客」に置き換えても、およその意味が通ると思います。

とあるように、データをただの数字として眺めるだけで終わらず、顧客そのものとして見えないものを見えるようにする力を養っていきたいところです。

付加価値の作り方

付加価値のつくりかた　一番大切なのに誰も教えてくれなかった仕事の本質

「価値とは何か？」というのはシンプルですが非常に難解な問題です。
ニーズに対して付加価値をつければそれがお金になる。当たり前のことであるのですが、ついつい自分たちがユーザに対してどのような付加価値を売っているのかというのは忘れてしまいがちです。
私たちのサービスが何であるのか、どんなにすごいのかも大切ではありますが、それがユーザにとってどんな価値をもたらすのかという観点を忘れないようにしたいですね。

行動経済学が最強の学問である

行動経済学が最強の学問である

行動経済学の本を何冊か読んだのですが、無難にこの1冊を。
行動経済学自体が比較的新しい学問で、経済学に心理学の要素を取り入れたような形です。古典的な経済学が人間は常に最良の行動をとるという前提に対して、どうやら人間は感情や思い込みといった要素によって思ったよりも非合理な行動を取りがちだぞみたいな話です。（雑な説明ですみません）
認知バイアスやナッジなどのときどき聞くようなワードが目に入りやすくなるし、何冊か読むと大体同じような話が登場するのである程度パターンを認識しておけそうです。
もちろんビジネスアイデアなどに活かすのもよいとは思いますが、知ってるからと言って回避できるような話でもないので、ふとした場面で自身の思考や行動にバイアスが掛かっているかもしれないと思いながらものごとと向き合うみたいな使い方が良いかなと思っています。

技術

ちょうぜつソフトウェア設計入門

ちょうぜつソフトウェア設計入門――PHPで理解するオブジェクト指向の活用

ゆるいイラストでタイトルにも「入門」と入っているので初心者向けの本かなと思っていたのですが、思った以上に本格的でした。
第1章が「クリーンアーキテクチャ」から始まる時点でだいぶビックリします。
DDDやオブジェクト指向といった内容が中心にはなるのですが、いわゆる解説本というよりは著者の考え方が洗練された文章で整理されており、非常に得るものが多かったです。またしばらくしたら読み直したいです。

アジャイルサムライ

アジャイルサムライ――達人開発者への道

アジャイル開発をするにあたっての良きハンドブックであり、アジャイル開発をしない場合でも十分に読む価値のある本だと思います。
というかアジャイルかそうじゃないかの境目ってそんなにはっきりしていないというかなんというか…。
イラストもなんだかおもしろく、文章も結構フレンドリーな感じなので読みやすいと思います。

毎週、価値ある成果を届けられているか？ たゆまぬ改善のための努力を惜しまず続けているか？ この2 つの問いヘの答えが「イエス」なら、君はアジャイルだ。

心はアジャイルでありたい。

システム設計の面接試験

システム設計の面接試験

面接試験とタイトルに入っているのですが、面接対策じゃなくてもいわゆるよくあるシステムってどういう構成で構築するものなのかみたいなユースケースがたくさん見られる良書です。
個別のミドルウェアをどう使うかみたいな情報は検索すればいろいろ出てくるのですが、「こういうパターンって普通はどうするんだ？」みたいなケースに対して体系的にまとまった情報はあまりなのでとてもありがたいです。

プリンシプルオブプログラミング

プリンシプル オブ プログラミング 3年目までに身につけたい 一生役立つ101の原理原則

内容的にそんなに目新しいものはないのですが、いわゆる「良いコード」って何みたいなところがうまく整理されている本です。
「3年目までに身に着けたい」とのサブタイトルの通り、早い時期に身に着けておけると良い内容が多く、比較的シンプルにまとまっているので組織としてのルール整備といった観点でも参考にできるように思います。

Azure OpenAI Serviceではじめる ChatGPT/LLMシステム構築入門

Azure OpenAI ServiceではじめるChatGPT/LLMシステム構築入門 エンジニア選書

LLM系で何を読むのがいいかというと難しいところなのですが、群雄割拠ではあるもののOpenAIの強さを見ても、現状では業務で利用するならAzureは無難な択なのではないかと思います。
いわゆるモデルの話からベクトル検索、そしてRAGというまず通る道を一通り解説しており、チャンクサイズのおすすめといったTipsもとりあえず使ってみたいというときにはありがたいと思います。
ただ、Azure AI Studioに統合されてそっちでやればいいのではといった感じになってきたので、やはりこの分野は賞味期限が短いなとは感じます。

パタン・ランゲージ

パタン・ランゲージ―環境設計の手引

エンジニアリングの本ではなく、建築の本ですがおまけとして。
GoFのデザインパターンに影響を与えた本です。Kindle版はありません。そして高いです。
組織やサービスのパタン・ランゲージをうまく集めることができたら、それを組み合わせてより大きなパターンを作れたりしないかなとかちょっと思っていたりします。

自己啓発

エフォートレス思考

エフォートレス思考 努力を最小化して成果を最大化する

エッセンシャル思考の続編です。エフォートレスは「気楽な」とか「気負わず」とかいったニュアンスですかね。

エッセンシャル思考は、「何を」やるかを教えてくれた。エフォートレス思考は、「どのように」やるかを極める技術だ。

どう頑張るかを追求するのもよいことですが、全部ではなく何を頑張るか、何を楽するかという考えも大切だなと改めて思いました。

Think clearly

Think clearly　最新の学術研究から導いた、よりよい人生を送るための思考法

よりよい人生を送るための思考法ということで、どう行動するかというよりは物事をどう捉えるかみたいな話が多いです。
もちろん自分の行動で変えられる出来事もたくさんあるとは思うのですが、そうでないことも世の中にはたくさんあります。
物事は変わらなくても捉え方を変えることによって気楽になれるならきっとその方がいいですよね。まぁそううまくいったら苦労はしないんですけどね。

限りある時間の使い方

限りある時間の使い方

人生って4000週間しかないんですって。なんだかそう聞くと短い気がしますよね。

「人はある年齢になると、衝撃的なことに、自分がどんな生き方をしようと誰も気にしていないことに気づく。人の期待に応えることばかり考え、自分を後回しにしてきた人にとって、これは非常に恐ろしい発見だ。自分のことを気にしているのは自分だけなのである」

どうせいつまでたっても手探りで、確信のないままやるしかないのだから、尻込みしていても仕方ない。待つのはもう終わりだ。今すぐに、やりたいことをやりはじめよう。知識や技術が足りなくてもかまわない。どうせ誰だって、あなたと同じようなものなのだから。

沁みますね。

答えを急がない勇気

答えを急がない勇気　ネガティブ・ケイパビリティのススメ

なんでも答えがすぐに出せて、すぐに出そうとするこの時代にあえて答えを出さないでおく。何かを「しないでおく」能力をネガティブ・ケイパビリティと呼ぶそうです。
ついつい不確定な中でも早く答えを出し、どんどん先に進んでいくポジティブ・ケイパビリティを我々は重要視しがちです。
もちろんそれが大切な場面も多くありますが、時に答えのないままに立ち止まり、答えを求め続ける力も大切にしないといけないなと思わされます。

メタ思考

メタ思考～「頭のいい人」の思考法を身につける

メタ思考、具体化、抽象化、物事を視座を上げたり下げたりスライドしたり、様々な目線で見ることは本質を捉えるためには重要な能力です。
本来私たちは個なのだから、究極的には一人称の視点しかもっていないのですが、それを訓練によって様々な視点に切り替えているわけですよね。
この本で紹介されている「エイリアス」として場面に応じた複数の自分の形を見出すという方法もそうですが、物事を客観視できるまさに「メタ思考」を持つことは強力な武器になりそうです。

というわけで

雑多ですが技術系は座学はちょっと少なめですかね。
手を動かしたり設計とかを考えていたような覚えはありますが。

いまは学習する組織を読んでいたりと、組織論とか物事の考え方みたいなところが最近はちょっと多かったかも。
行動経済学系の本は他にも何冊か読みましたが、割と好きかもしれないです。

ペース早めに読んでいますが、数を読むことを目標にしないように気をつけねば…。
みなさんも良き読書ライフを。

それでは。

Remix+Prisma+Storybookでお手軽Webアプリ

こんにちは。
まだ梅雨入りもしていないですが、そろそろ夏が来たって感じがしますね。

さて、せっかくRemixのチュートリアルをやったので試しにWebアプリを作ってみます。
今回はORMとしてPrismaを、UIコンポーネントの確認ツールとしてStorybookを使います。
お手軽と書いてはみたものの、それなりに悩んだり躓いたりしたので、そのあたりをメインに記事にします。

今回作ったものはこちらのGitHubリポジトリにコードの全量があるので、よろしければどうぞ。
あくまで学習目的のため、例えばチェック処理がまるっとないなどご了承ください。（気が向いたら機能追加します）

github.com

ちなみにこんな感じのレシピを管理するためのアプリになっています。（白ご飯.comさんの画像そのまま使わせてもらっています）

こっちは登録画面。

Remixまわりのあれこれ

コンポーネントの置き場所と書き方

チュートリアルでは「app/routes」下に全部のtsxファイルが収まっています。
実際には単体ではページとして利用しない通常のコンポーネントを作ることになるかと思いますので、これをどこに置くのかがちょっと悩みました。

答えとしては「app/components」みたいなディレクトリを作るで問題ありません。
「app/routes」下にファイルを作ってしまうとRemixが勝手にパスを生成してくれてしまうので注意です。
ちなみにFormなどのRemixコンポーネントは普通に利用できますが、エントリポイントではないのでloaderやactionは書けないので注意です。

ベースパスの変更

リバースプロキシの背後にアプリを置く場合などにベースのパスを変更することになりますが、これもちょっとハマりました。
結論としてはvite.config.tsを以下のような設定にします。

export default defineConfig({
  base: "/recipe/",
  plugins: [
    remix({
      basename: "/recipe/",
      future: {
        v3_fetcherPersist: true,
        v3_relativeSplatPath: true,
        v3_throwAbortReason: true,
      },
    }),
    tsconfigPaths(),
  ],
});

viteの設定であるbaseとremixの設定であるbasenameの両方に値を設定しないといけないのがポイントです。
調べたら出てきた設定を片方ずつ反映して、どっちもうまくいかないと困惑していました。

複雑なPOST

Remixはformを使ってWeb標準っぽくリクエストが投げられるのが素敵なのですが、それなりに複雑なデータをPOSTする場合にどうするのかちょっと悩みました。
通常の値を取得する際にはこんな感じでformDataからgetでデータを取得します。

const formData = await request.formData();
console.log(formData.get("hoge"));  // hoge

同じ値が複数取れる場合にはgetAllで配列で取れます。

const formData = await request.formData();
console.log(formData.getAll("fuga")); // [ "fuga1", "fuga2" ]

が、複雑な構造になってくるとgetAllで取得したものをzipして要素を作っていくのはちょっと怪しそうです。
そういう場合には普通にuseStateを使ってオブジェクトを管理し、useSubmitを使ってsubmit時にJSON化して送ってしまうのがシンプルそうです。

const  submitMenu = // 略
submit({ "json": JSON.stringify(submitMenu), "type": "update" }, { method: "post" });

受け取る側はJSON.parseで復元します。

const menu = JSON.parse(formData.get("json")!.toString()) as MenuAll;

Prismaまわりのあれこれ

migrateの挙動

Prismaを使う場合、既存のDBから情報を取ってくる「prisma db pull」と、Prisma側からDBを更新する「prisma migrate」のどちらを使うかというところが最初に気になります。
特にmigrateは破壊的な挙動になるので、間違った知識で実行してしまうと大変な事故になりかねないので挙動を確認しました。
結論から言えば、対象のデータベース（スキーマ）をこのアプリケーション用に新しく作るのであればmigrateをメインに使い、そうじゃない場合にはやめたほうが良さそうだなという感覚です。
（もちろん十分に気をつけてちゃんと管理すれば既存のデータベースに対しても利用できるとは思います）

通常、Prismaは接続先のデータベースのすべてを対象にします。なので、例えば「prisma db pull」で全テーブルの定義を引っ張ってきて必要なテーブルだけを残し、「prisma migrate」を実行すると他のテーブルは消えます。
しかもすごく恐ろしい話なのですが、「--create-only」というオプションを付けると安全なように見えて、同様に消えます。怖い。
そして、テーブルに変更がなくても初回にmigrateした時点でテーブルが作り直されてデータは消えます。怖い。
バックアップして戻すみたいな運用をする感じなのでしょうか。大量にデータが入っててレプリケーションとかしてる場合結構つらそう…。

DB定義を直接変更して「prisma db pull」してきたあとでも同じことが起きると思うので、migrateを使う場合にはDB定義を必ずPrisma経由に徹底する必要がありそうですね。
ちなみに定義情報はアプリケーションではなく自動生成される「_prisma_migrations」テーブルに保存されるので、Prismaで統一さえしていれば複数のアプリケーションで触ってもOKとかあるんでしょうか。未検証です。
なんか思ったよりmigrateを使うのが難しそうなので、なにか勘違いしていることがあるかもしれないです。今度改めて細かいことも確認してみたいです。

型をそのまま使ってしまいがち

全体的な感想としては型がガッツリ効くのがすごく良い感じです。
例えばこんな風に書くと、

const result = await prisma.menu.findUnique({
    where: { menuId: menuId },
});

こういう型で返ってくるのですが、

const result: {
    menuId: number;
    name: string;
    imageUrl: string | null;
} | null

こんな感じでincludeの指定をすると、

const result = await prisma.menu.findUnique({
    where: { menuId: menuId },
    include: { 
        steps: true,
        tags: true,
        links: true,
    },
});

型が変わります。

const result: ({
    links: {
        menuId: number;
        url: string;
        title: string;
    }[];
    steps: {
        menuId: number;
        seqNo: number;
        text: string;
    }[];
    tags: {
        menuId: number;
        tag: string;
    }[];
} & {
    menuId: number;
    name: string;
    imageUrl: string | null;
}) | null

ただ、Prismaがネストしたモデルを自動生成してくれるので、ついついそのまま画面側まで持っていってしまいたい気持ちになります。
今回まさにそうしてしまったのですが、これは素直にちゃんと型変換をしたほうがいいと思います。
includeの指定で返却される型が動的に変わる機能はとても素敵なのですが、無名の直積型のような型（？）で返ってくるので、DBから遠いところまでそのまま持っていくと型のエラーが何を言っているのかが正直全然良くわかりません。

どんなクエリが発行されているか謎い

普通にSQLを書いたら1回で取ってくるようなデータも別々のクエリで引っ張ってきて合体させているような挙動をよく取りがちです。
previewFeaturesのrelationLoadStrategyとかを使うとjoinを使ってくれるようになるようですが、ひとまずはどんなクエリが発行されているかは1回は確認しておいたほうが良いと思います。

PrismaClientを作成する際のオプションに以下のように設定すると、ログに発行するクエリが出るので随時確認しておきたいところです。

const prisma = new PrismaClient({
    log: ['query'],
});

なかなかがっつりなクエリです…。

prisma:query SELECT `db`.`menu`.`menuId`, `db`.`menu`.`name`, `db`.`menu`.`imageUrl` FROM `db`.`menu` WHERE (`db`.`menu`.`menuId` = ? AND 1=1) LIMIT ? OFFSET ?
prisma:query SELECT `db`.`menu_ingredient_group`.`menuId`, `db`.`menu_ingredient_group`.`groupId`, `db`.`menu_ingredient_group`.`groupName` FROM `db`.`menu_ingredient_group` WHERE `db`.`menu_ingredient_group`.`menuId` IN (?)
prisma:query SELECT `db`.`menu_ingredient`.`menuId`, `db`.`menu_ingredient`.`groupId`, `db`.`menu_ingredient`.`seqNo`, `db`.`menu_ingredient`.`name`, `db`.`menu_ingredient`.`amount` FROM `db`.`menu_ingredient` WHERE (`db`.`menu_ingredient`.`menuId`,`db`.`menu_ingredient`.`groupId`) IN ((?,?),(?,?),(?,?))
prisma:query SELECT `db`.`menu_step`.`menuId`, `db`.`menu_step`.`seqNo`, `db`.`menu_step`.`text` FROM `db`.`menu_step` WHERE `db`.`menu_step`.`menuId` IN (?)
prisma:query SELECT `db`.`menu_tag`.`menuId`, `db`.`menu_tag`.`tag` FROM `db`.`menu_tag` WHERE `db`.`menu_tag`.`menuId` IN (?)
prisma:query SELECT `db`.`menu_link`.`menuId`, `db`.`menu_link`.`url`, `db`.`menu_link`.`title` FROM `db`.`menu_link` WHERE `db`.`menu_link`.`menuId` IN (?)

Storybookまわりのあれこれ

エラーです

npx storybook@latest init

でインストール自体は問題なく進むのですが、起動するといきなりエラーになります。

github.com
このあたりのページを参考にしましたが、どうやらViteをサーバに使ったRemixではvite.config.tsの設定を変えてあげる必要があるらしいです。

sb-vite.config.tsというファイルを別途作成して中身は以下の通りにします。

import { defineConfig, loadEnv } from 'vite';
import tsconfigPaths from 'vite-tsconfig-paths';

export default defineConfig(({ mode }) => {
  const env = loadEnv(mode, process.cwd(), '');
  process.env = { ...process.env, ...env };
  return {
    plugins: [tsconfigPaths()],
  };
});

そして.storybook/main.tsを以下の通り更新します。読み込ませる設定を変更するのと、storiesを更新してapp下のファイルを探すようにします。

import type { StorybookConfig } from "@storybook/react-vite";

const config: StorybookConfig = {
  stories: [
    "../app/**/*.stories.@(js|jsx|ts|tsx)"
  ],
  addons: [
    "@storybook/addon-onboarding",
    "@storybook/addon-links",
    "@storybook/addon-essentials",
    "@chromatic-com/storybook",
    "@storybook/addon-interactions",
  ],
  framework: {
    name: "@storybook/react-vite",
    options: {
      builder: {
        viteConfigPath: 'sb-vite.config.ts',
      },
    },
  },
};
export default config;

さらにRemixのコンポーネントをスタブにする必要があるため、対象のstoriesファイルでdecoratorsを指定します。
例えばこんな感じです。ユニットテストを書く場合にも同様にスタブ化する感じでしょうか。

const meta: Meta<typeof Sidebar> = {
    component: Sidebar,
    title: 'Sidebar',
    decorators: [
        Story => {
            const Stub = createRemixStub([
                {
                    path: '/',
                    Component: () => <Story />, 
                },
            ]);
            return <Stub />;
        },
    ],
};
export default meta;

スタイルが効かない

とりあえず表示できるようになったのですが、CSSを読み込んでいないのでスタイルが効きません。

import "../styles/common.css";

のように書くとcssファイルが読み込めます。
今回でいうと.containerのスタイルも併せて反映させたいので、Storyコンポーネントをwrapしてあげます。

Story => {
    const Stub = createRemixStub([
        {
            path: '/',
            Component: () => <div className="container"><Story /></div>, 
        },
    ]);
    return <Stub />;
},

routes下の場合の設定

コンポーネントの場合はデータは引数で受け取るので上記までで問題なのですが、routes下の場合にはloader関数がないとデータが取れなくてエラーになってしまいます。
その場合はdecoratorsに更にloader関数を足してあげます。

export const Empty: Story = {
    decorators: [
        Story => {
            const Stub = createRemixStub([
                {
                    path: '/',
                    loader: () => ({
                        menu: { 
                            menuId: 1, 
                            name: "メニュー1", 
                            steps: [] as MenuStep[], 
                            tags: [] as MenuTag[], 
                            links: [] as MenuLink[],
                            ingredientGroups: [] as IngredientGroup[],
                        } as MenuAll,
                        buttonName: "登 録",
                    }),
                    Component: () => <div className="container"><Story /></div>,
                },
            ]);
            return <Stub />;
        },
    ],
};

CSSが全部読み込まれる

importを使ってコンポーネントごとに別々のCSSを読み込んでいるつもりなのですが、よく見ると全部のコンポーネントのCSSがまとめて読み込まれてしまっています。
互いに干渉しなければこのままでもいいのですが、そうじゃない場合には困ります。とりあえず名前付きでimportしてstyleタグに直接書き込むという方法でなんとかなりましたが、本当にこれでいいのかはとても謎です。

import menuCss from "../styles/menu.css?raw";

// 略

export const Empty: Story = {
    decorators: [
        Story => {
            const Stub = createRemixStub([
                {
                    path: '/',
                    loader: () => ({
                        menu: { 
                            menuId: 1, 
                            name: "メニュー1", 
                            steps: [] as MenuStep[], 
                            tags: [] as MenuTag[], 
                            links: [] as MenuLink[],
                            ingredientGroups: [] as IngredientGroup[],
                        } as MenuAll
                    }),
                    Component: () => 
                        <>
                            <style>${menuCss}</style>
                            <div className="container"><Story /></div>
                        </>,
                },
            ]);
            return <Stub />;
        },
    ],
};

終わりに

そんなに高機能なアプリじゃないのですが、知らないことが多かったのでなんだかんだ時間がかかりました。
ただ、作りたいものに対してうまくいかないをなんとかするというのが一番理解が進む瞬間だと思うので、簡単なものでもいいからこういうのが作りたいと思って手を動かすのが良いと思います。

それぞれ単品でも便利に使えるものなので、うまく使っていければと思います。
それでは。